안녕하세요! 다들 추석 연휴 잘 보내셨는지 모르겠습니다..ㅎㅎ
저는 잘 지내고 왔지만 이틀 동안 블로그 작성을 쉬었네용 많은 분들이 기다렸을 것 같은데(?)
오늘도 재밌는 이야기로 시작해볼까요^_^?
오늘은 전자공학에 관한 기초내용입니다. 아직 기초내용을 다루기 때문에 많은 분들이 쉽게 익히실 수 있을 것 같습니다.
V=IR?
V=IR이라는 식을 많이 접하셨을텐데요 ㅎㅎ 이 공식은 옴의 법칙이라고 불립니다.
독일의 과학자 게오르그 옴의 이름을 따서 지어준 이름이라네요. 먼저 이 식을 이해하기전에 아주 기초로 돌아가보면
전류
제가 올려놓은 화학 글들에서도 알 수 있듯이 원자 내부에는 전자가 존재하는데요, 이러한 전자가 도체 내부에서 흐르면
물리적인 일을 할 수 있게 됩니다. (물리적인 일은 나중에 다루도록 하겠습니다..) 이러한 전자의 흐름을 '전류' 라고 합니다.
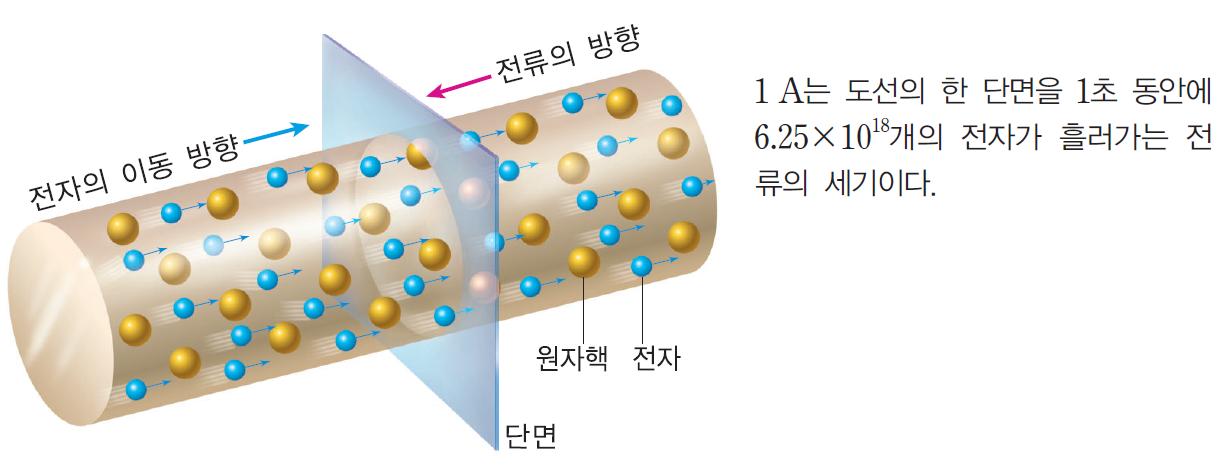
전류의 방향은 (+) ------> (-)랍니다. 전류의 단위는 A(암페어)를 씁니다. 전류는 전자의 이동 방향과 반대인데요.
왜 그렇냐고 물어보면 당시에 과학자들에게는 '전자'라는 개념이 없었기 때문에 단순히 (+)에서 (-)로 약속을 했기 때문입니다. 그렇다면 '전류는 왜 흐르는가?' 라는 질문을 던질 수가 있는데요. 전류는 왜 흐를까요?
(* 1암페어는 두 도선에 전류가 흐를 때 지름을 무시할 수 있고 길이가 무한한 두 직선 도선이 서로 1m 떨어져 있고,
같은 크기의 전류가 흐를 때 1m 당 2*10^-7N의 힘이 작용한다면 두 도선에 흐르는 전류는 1A입니다.)
전압
흔히 전자의 흐름을 물의 흐름과 비유해서 쓰는데 전압 역시 마찬가지로 물의 흐름에 빗대어 표현하면 쉽게 이해할 수 있습니다. 전압은 보통 전지에 의해 발생하는 '전위 차'입니다. 전압의 단위는 V(볼트)를 씁니다.

위 그림에서 물통A로 물의 높이를 끌어올려주는 펌프의 역할을 하는게 '전지'라고 이해하면
전지에 의해 전위차가 발생해 전류가 흐르는 것을 알 수 있습니다.
(* 1V는 1A의 전류가 도체의 두 점 사이를 흐를 때 소모되는 전력이 1W일 때 그 두 점 사이의 전압으로 정의합니다.)
저항
일반적으로 전류가 흐르는 도선에 저항이 발생한답니다. 도선 속의 전자가 도선을 이동하면서 원자와 충돌하기 때문에
열도 발생합니다. 도선의 단면적이 클수록 저항이 작으며 도선의 길이가 짧을수록 저항이 작습니다.

그림에서 볼 수 있듯이 사람이 더 편하게 지나다니기 쉬운 길은 단면적이 큰 길이죠? 또한
도선이 짧으니까 당연히 더 편하게 지나갈 수 있습니다. 이는 전자에게도 마찬가지인거죠 ㅎㅎ
저항의 단위로는 Ω(옴)을 사용합니다.
I=V/R다시 돌아와서 옴의 법칙에 관해 이야기해볼까요? 옴의 법칙은 앞서 과학자 옴이 발견한 법칙입니다.전자공학의 기초가 되는 식이자 이 식의 참된 의미는 바로 '이것' 입니다.' 도선에 흐르는 전류는 전압에 비례하고 저항에 반비례한다. 즉 전압이 클수록 전류의 세기가 세고, 저항이 클수록 전류의 세기가 약해진다. '

또한 옴은 여러가지 금속으로 회로를 만들어 실험을 했는데 각각의 금속이 지닌 고유한 성질에 따라 전류가 많이 흐르거나 적게 흐르는 것을 발견해 전기저항에 관한 정의도 내립니다!
마지막으로 저항의 직렬연결과 병렬연결에 대해 알아보겠습니다.
저항의 직렬연결
전기 회로에서 여러 개의 저항을 직렬로 연결한 것을 말 그대로 '직렬 연결'이라고 합니다.
직렬로 연결했을 때 회로에 걸리는 전체 저항의 크기는 각각의 저항값을 모두 더한 값과 같습니다.

위 그림에서 전류의 세기를 계산해볼까요? 저항을 직렬로 연결했기 때문에 전체 저항의 크기는 2+4 = 6 (옴) 입니다.
전류의 세기 I = 12V/6Ω 이므로 2A의 전류가 흐르겠네요!

저항의 직렬연결을 아주 이해하기 쉽게 그려놓은 그림입니다. 전위차가 각각의 저항(물레방아)을 지나가면서 줄어들죠?
이와 마찬가지로 직렬연결에서 각 저항에 걸리는 전압이 제 각각 다르고 마지막에 전위가 0에 다다르는 걸 알 수 있네요.
저항의 병렬연결은 어떨까요?
저항의 병렬연결
전기 회로에서 여러 개의 저항을 병렬로 연결한 것을 '병렬 연결'이라고 합니다.
병렬로 연결했을 때 회로에 걸리는 전체 저항의 크기는 ' 각각의 저항값의 역수를 모두 더한 값의 역수와 같습니다. '
위의 말이 잘 이해가 안되실텐데요. 이는 옴의 법칙을 통해 증명이 가능합니다. 먼저 회로부터 볼까요?

위 그림에서 회로의 전류를 계산해볼까요?
그 전에 저항의 병렬연결에 대한 그림을 먼저 보고가면 이해가 더 쉬울거에요.

보시다시피 저항(물레방아)에 같은 전압(전위차, 높이차)이 걸리는 것을 알 수 있습니다. 따라서 위 그림을 다시보면

3Ω과 6Ω에 걸리는 전압은 각각 6V이므로
3Ω의 저항일때는 I=6V/3Ω , 2A입니다.
또한 6Ω의 저항일때는 I=6V/6Ω , 1A입니다. 도선에 각각 2A, 1A의 전류가 흐르다가 한 곳에서 만나죠?
그래서 도선 전체에 흐르는 전류의 크기는 3A임을 알 수 있습니다.
다른 방법으로 '위의 말'을 이해해봅시다.
저항의 병렬연결에서 걸리는 전압의 크기는 모두 같기 때문에 저항 1과 저항 2에 걸리는 전압을 각각 V1, V2라고 하면
걸어준 전압, V=V1=V2 (주어진 조건) 입니다. (저항의 수는 관계없이 증명이 가능합니다. 편의를 위해 2개로 잡았습니다.)
V=IR에서
I(전체 전류)=I1(저항 1에 흐르는 전류) + I2(저항 2에 흐르는 전류)
V(전체 전압)/R(전체 저항) =V1/R1 + V2/R2
주어진 조건을 사용하여
1/R(전체 저항) = 1/R1 + 1/R2 입니다. 따라서 '위의 말'을 증명할 수 있게 됩니다!
마지막 저항의 병렬연결은 식을 사용해야하는데 문자로 표현하니까 이해하기도 어렵고 복잡하죠? 이럴 때 정말
수식의 귀중함을 깨닫게 되는 것 같습니다..ㅎㅎ 선대 과학자들과 수학자들이 남긴 이런 업적들을 배우고 발전시켜
앞으로 후대에 그 뜻을 전하는게 저희의 역할이 아닐까요? 저도 그들 중 한 명이 되고자 이 글을 쓰고 있는 것 같습니다.
오늘도 재밌게 읽으셨으면 좋겠고 추석도 끝났으니 다시 한 번 현생으로 돌아가 화이팅합시다! 감사합니다 :)
사진 출처: 한국전력공사 공식 홈페이지, 중학교 2-2 교과서, 티스토리 - 달빛과학, 구글
'과학' 카테고리의 다른 글
| 화학_화학 결합(Chap.3 금속결합) (0) | 2022.09.08 |
|---|---|
| 화학_화학 결합(Chap.2 공유결합) (0) | 2022.09.07 |
| 화학_화학 결합(Chap.1 이온 결합) (3) | 2022.09.06 |


